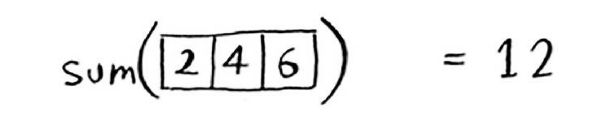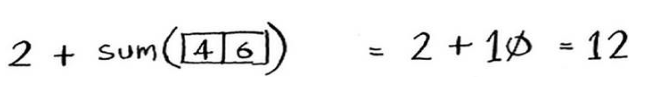分而治之是一种算法思维，而不是具体的某个算法实现。
概念
分而治之（divide and conquer，D&C），并没有严格的一个概念，但是从《算法图解》和《算法导论》中对分而治之的解释中，可以总结出以下解释：将原问题分解为几个规模较小但类似于原问题的子问题，递归地求解这些子问题，然后在合并这些子问题的解来建立原问题的解。
从上面的解释中我们可以看出，分而治之的思维是靠递归来实现的，所以说，分而治之是一种思维，而递归就是具体的实现。我们经常提的二分法也都是分而治之思维的实践。包括排序算法中最快的算法之一的快速排序算法就是分而治之的一个经典实现。
分而治之的实现具体有2个步骤：
1.找出基线条件，这种条件必须尽可能简单
2. 不断将问题分解（或者说缩小规模），直到符合基线条件。
案例
下面，我们通过两个具体的案例来详细介绍下分而治之。
（一）
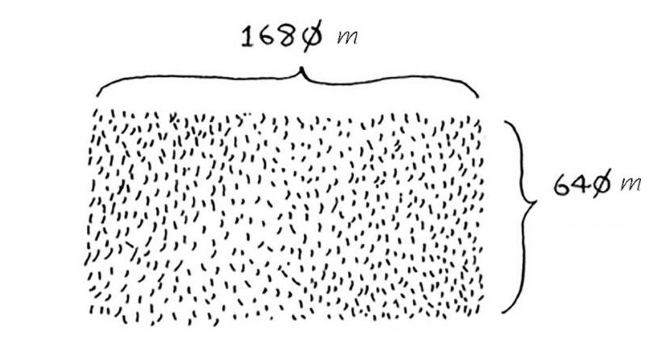
假设你是农场主，有一小块土地。
你要将这块地均匀地分成方块，且分出的方块要尽可能大。
如何将一块地均匀地分成方块，并确保分出的方块是最大的呢？使用 D&C策略！
下面就来使用D&C找出前述问题的解决方案。可你能使用的最大方块有 多大呢？
首先，找出基线条件。最容易处理的情况是，一条边的长度是另一条边 的整数倍。
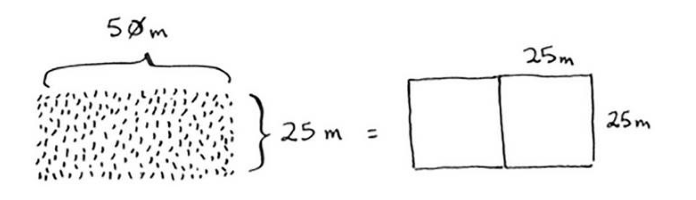
如果一边长25 m，另一边长50 m，那么可使用的最大方块为 25 m×25 m。换言之，可以将这块地分成两个这样的方块。 现在需要找出递归条件，这正是D&C的用武之地。根据D&C的定义， 每次递归调用都必须缩小问题的规模。如何缩小前述问题的规模呢？我 们首先找出这块地可容纳的最大方块。
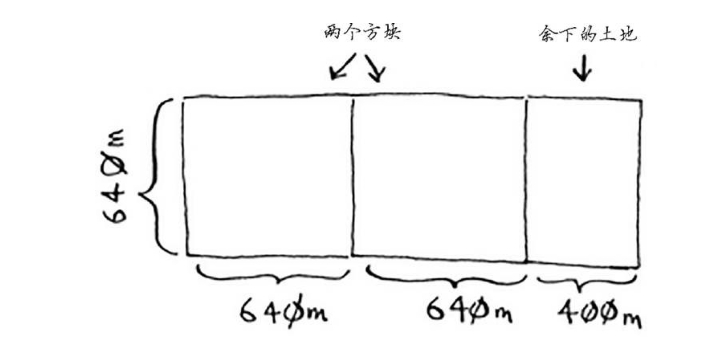
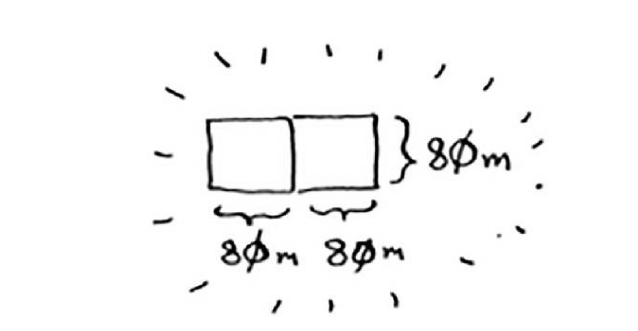
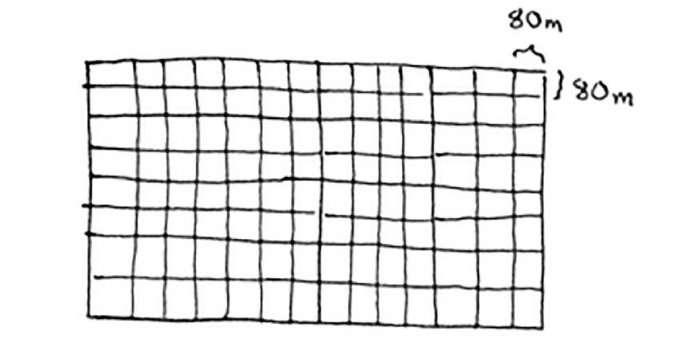
你可以从这块地中划出两个640 m×640 m的方块，同时余下一小块地。 现在是顿悟时刻：何不对余下的那一小块地使用相同的算法呢？
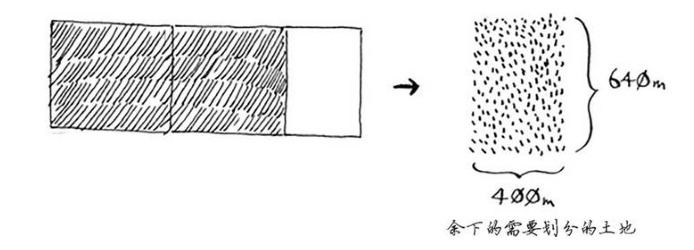
最初要划分的土地尺寸为1680 m×640 m，而现在要划分的土地更小，为 640 m×400 m。适用于这小块地的最大方块，也是适用于整块地的最大方块 。换言之，你将均匀划分1680 m×640 m土地的问题，简化成了均 匀划分640 m×400 m土地的问题！
“适用于这小块地的最大方块，也是适用于整块地的最大方块 。” 这句话可能比较难理解，如果不理解，可以参考欧几里得算法。这个其实是根据欧几里得算法推导出来的。
根据这个思路，我们继续对“较小”的地块进行分解，最终会得到最大满足条件的正方形。
最终，我们求出适用的最大方块为80 m× 80 m。
（二）
我们再来看一个例子
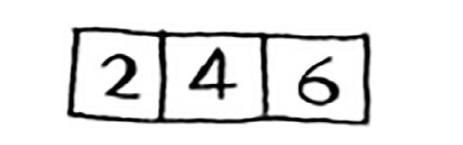
给定一个数组
你需要将这些数字相加，并返回结果。使用循环很容易完成这种任务。
但如何使用递归函数来完成这种任务呢？
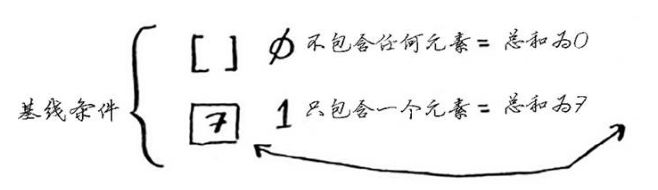
第一步 ：找出基线条件。最简单的数组什么样呢？请想想这个问题， 再接着往下读。如果数组不包含任何元素或只包含一个元素，计算总和 将非常容易。
因此这就是基线条件。
第二步 ：每次递归调用都必须离空数组更近一步。如何缩小问题的规
模呢？下面是一种办法。
这与下面的版本等效。
这两个版本的结果都为12，但在第二个版本中，给函数sum 传递的数组 更短。换言之，这缩小了问题的规模 ！
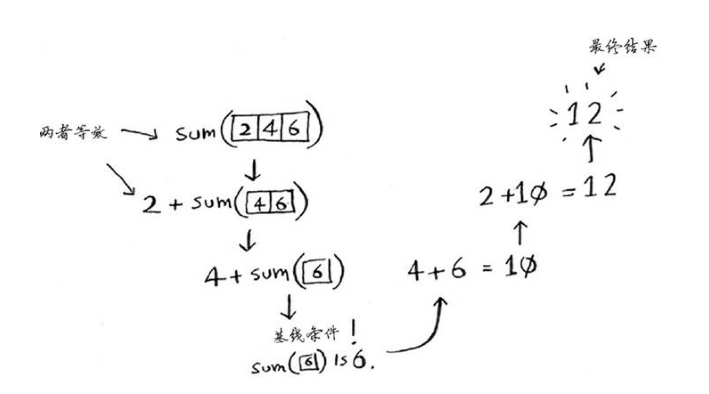
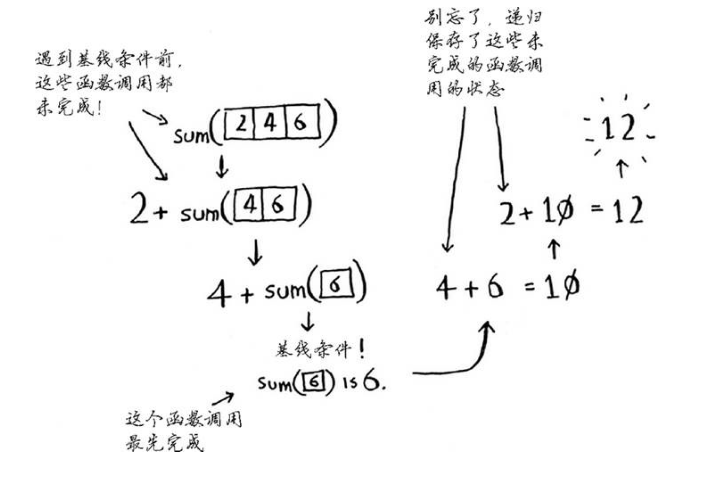
这个函数的运行过程如下。
递归记录了状态。遇到基线前，这些函数调用都未完成。
分而治之的经典实现–快速排序算法
动画演示：
function quickSort($arr){
if(count($arr)<=1){
return $arr;
}
$middle = $arr[0];
$left = [];
$right = [];
for($i=1;$i<count($arr);$i++){
if($arr[$i] < $middle){
$left[] = $arr[$i];
}else{
$right[] = $arr[$i];
}
}
return array_merge(quickSort($left),array($middle),quickSort($right));
}
参考文献：
1.《算法图解》.Aditya Bhargava .[译]袁国忠
2.《算法导论(第3版)》